L'approccio indicato nella domanda è un po' complesso da implementare; a meno che non ci sia qualche motivo particolare per utilizzarlo, per lo specifico caso in oggetto, si può utilizzare un metodo alternativo basato sugli angoli individuati dalle rette passanti per i vertici che definiscono lo "pseudo cerchio" e l'asse "X" e, analogamente, quelli delle rette passanti per i punti "random".
La retta passante per l'n-esimo punto random intercetterà la retta passante per i due vertici consecutivi dello "pseudo cerchio" ai quali corrisponderanno un angolo maggiore ed un minore rispetto a quello relativo alla retta passante per il numero random.
figure('position',[470 235 560 420]);
%
% Flag abilitazione plot intermedi (per debug)
%
en_plot=1;
%
% Definizione numero punti pseudo cerchio
% Generazione punti e plot del "pseudo cerchio"
%
n_punti=15;
a=0:2*pi/n_punti:2*pi;
n_c=length(a);
x=cos(a);
y=sin(a);
plot(x,y)
grid on
xlim([-1.3 1.3]);
ylim([-1.3 1.3]);
% daspect([1 1 1]);
hold on
%
% Generazione "punti random": il numero di punti generati è (n_pt*2)
%
n_pt=4;
n_pt_2=n_pt*2;
z=[rand(n_pt,1) rand(n_pt,1)*-1];
z=z(randperm(n_pt_2));
t=[rand(n_pt,1) rand(n_pt,1)*-1];
t=t(randperm(n_pt_2));
%
% Calcolo angoli dei punti random
% varaibile "ang_p"
% La funzione "atan2" restituisce valori negativi per punti nel 3° e 4°
% quadrante, aggiungendo "360" si ottine il valore dell'angolo tra (0;360)
%
ang_p=zeros(n_pt_2,1)*NaN;
for i=1:n_pt_2
tmp=atan2(t(i),z(i))*180/pi;
if(tmp < 0)
tmp=tmp+360;
elseif(tmp == 360)
tmp=0;
end
ang_p(i)=tmp;
if(en_plot)
P(i)=plot(z(i),t(i),'d','markerfacecolor','r','markeredgecolor','r');
end
end
%
% Calcolo angoli dei punti pseudo cerchio
% varaibile "ang_c"
% La funzione "atan2" restituisce valori negativi per punti nel 3° e 4°
% quadrante, aggiungendo "360" si ottine il valore dell'angolo tra (0;360)
%
ang_c=zeros(n_c,1)*NaN;
for i=1:n_c
tmp=atan2(y(i),x(i))*180/pi;
if(tmp < 0)
tmp=tmp+360;
elseif(tmp == 360)
tmp=0;
end
ang_c(i)=tmp;
if(en_plot)
C(i)=plot(x(i),y(i),'o','markerfacecolor','g','markeredgecolor','g');
end
end
%
% Cancellazione elementi plottati (solo per debug)
%
if(en_plot)
delete([P, C]);
clear P C
end
%
% Definizione elementi ascissa per il successivo plot delle rette
%
tmp_x=-2:.3:2;
%
% Inizializzazione vettori e cell array di output
% X= ascissa del punto di intersezione
% Y= ordinata del punto di intersezione
% RES_IDX= indice del primo punto del pseudo cerchio con angolo superiore a
% quello dell'i-esimo punti random
%
X=zeros(n_pt_2,1)*NaN;
Y=zeros(n_pt_2,1)*NaN;
RES_IDX=zeros(n_pt_2,1)*NaN;
%
% Calcolo del punto di intersezione:
% Loop esterno sui punti random
%
for i=1:n_pt_2
if(en_plot)
P=plot(z(i),t(i),'d','markerfacecolor','r','markeredgecolor','r');
end
%
% Controllo caso particolare: lo i-esimo punto random ha un angolo
% superiore all'ultimo di quelli definitri per lo pseudo cerchio
%
if(ang_p(i) >= ang_c(end))
j=1;
C(j)=plot(x(j),y(j),'o','markerfacecolor','g','markeredgecolor','g');
else
j=1;
%
% Loop interno sui punti dello pseudo cerchio Ricerca dell'j-esimo
% punto dello pseudo cerchio con angolo maggiore a quello dello
% i-esimo punto random
% Ogni ciclo interno termina quando:
% viene trovato il punto dello pseudo cerchio con angolo
% maggiore a quello del punto random oppure quando sono
% stati esaminati tutti i puni dello pseudo cerchio
%
while(j < n_c)
if(ang_p(i) >= ang_c(j))
if(en_plot)
C(j)=plot(x(j),y(j),'o','markerfacecolor','r','markeredgecolor','g');
R(j)=plot([0 cos(ang_c(j)*pi/180)],[0 sin(ang_c(j)*pi/180)]);
end
j=j+1;
else
break;
end
end
end
%
% Salvataggio dei risultati nei vettori di output
%
if(j == 1)
RES_IDX(i)=1;
idx_1=n_c;
idx_2=1;
else
RES_IDX(i)=j;
idx_1=j-1;
idx_2=j;
end
%
% Plot dei risultati (solo per debug)
%
if(en_plot)
C(idx_2)=plot(x(idx_2),y(idx_2),'o','markerfacecolor','g','markeredgecolor','g');
R(idx_2)=plot([0 cos(ang_c(idx_2)*pi/180)],[0 sin(ang_c(idx_2)*pi/180)]);
[ang_c(idx_1) ang_p(i) ang_c(idx_2)]
end
%
% Calcolo parametri della retta passante per i due vertici correnti del
% poligono e della retta passante per il punto random
%
mc=(y(idx_2)-y(idx_1))/(x(idx_2)-x(idx_1));
kc=-mc*x(idx_1)+y(idx_1);
mp=(t(i)-0)/(z(i)-0);
kp=0;
%
% Plot delle rette
%
if(en_plot)
tmp_y=tmp_x*mc+kc;
RC=plot(tmp_x,tmp_y,'r');
tmp_z=-2:.3:2;
tmp_t=mp*tmp_z+kp;
if(t(i) >= 0)
m=find(tmp_t < 0);
else
m=find(tmp_t > 0);
end
tmp_z(m)=[];
tmp_t(m)=[];
RP=plot([0 tmp_z],[0 tmp_t],'k');
TMP_Z{i}=tmp_z;
TMP_T{i}=tmp_t;
end
%
% Calcolo del punto di intersezione delle rette (metodo di Cramer)
%
D=(-mc+mp);
if(D ~= 0)
X(i)=(kc-kp)/D;
Y(i)=(-mc*kp+mp*kc)/D;
if(en_plot)
XY=plot(X(i),Y(i),'s','markerfacecolor','b');
end
else
error(['No intersection z=' num2str(z(i)) ' t=' num2str(t(i))])
end
%
% Gli oggetti plottati vengono cancellati prima di passare
% all'iterazione successiva
%
if(en_plot)
delete([P C R RC RP XY]);
clear P C R RC RP XY
end
%
% Fine del loop esterno sui numeri random
%
end
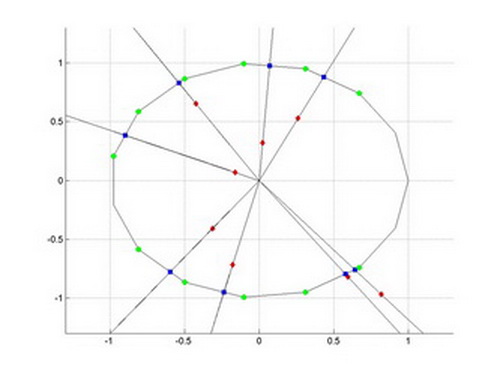
%
% Plot dei risultati finali
%
figure('position',[470 235 560 420]);
axes
grid on
xlim([-1.3 1.3]);
ylim([-1.3 1.3]);
hold on
plot(x,y,'k')
for i=1:n_pt_2
plot([x(RES_IDX(i))],[y(RES_IDX(i))],'o','markerfacecolor','g','markeredgecolor','g');
plot([x(RES_IDX(i)-1)],[y(RES_IDX(i)-1)],'o','markerfacecolor','g','markeredgecolor','g');
plot(z(i),t(i),'d','markerfacecolor','r','markeredgecolor','r');
plot(X(i),Y(i),'s','markerfacecolor','b','markeredgecolor','b');
plot([0 TMP_Z{i}],[0 TMP_T{i}],'k');
end
Allegati:
 16082_819b8baa6f90fb860b9e6cbce40ecc06.jpg
16082_819b8baa6f90fb860b9e6cbce40ecc06.jpg