Non è chiaro quali siano i dati di input.
Se non ci sono vincoli sui dati di input, una soluzione molto semplice potrebbe essere:
[*] definire il centro (un vettore di due elementi: x e y, c=[0 0]) ed il raggio della circonferenza (una variabile: r=3 ad esempio)
[*] definire due vettori (analogamente al centro della circonferenza) per la posizione dei due estremi della curva. Per semplificare il tutto, i due punti potrebbero avere la stessa ordinata del centro della circonferenza. L'ascissa del punto a sinistra della circonferenza sarà "un po' di meno della coordinata del centro - il raggio", quello a destra, "un po' di più della coordinata del centro + il raggio"
[*] puoi definire altri due punti per i quali dovrà passare la curva come, rispettivamente, i due punti intermedi tra la circonferenza ed i punti esterni (anche questi come vettori di due elementi) per quanto riguarda l'ascissa. Le ordinate dei due punti basta che siano superiori al raggio (se hai scelto i punti iniziali alla stessa ordinata del centro)
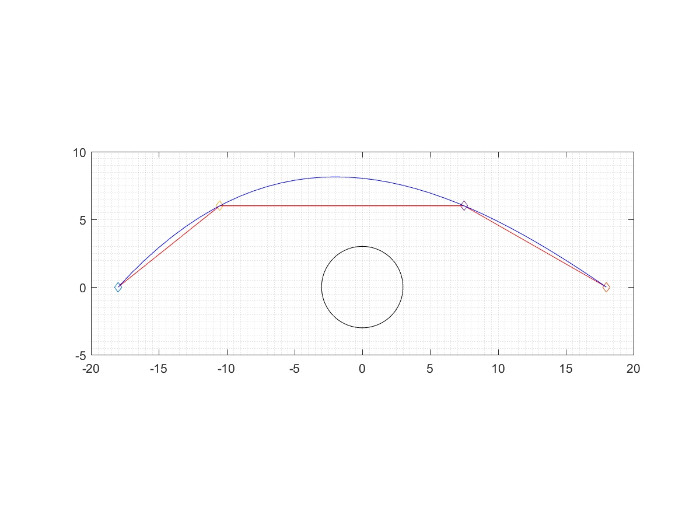
[*] adesso hai quattro punti che puoi unire con una spezzata (usando la funzione plot per plottarli) oppure puoi creare una spline che passi per i quattro punti
Esistono molte altre possibili soluzioni, un po' più elaborate dal punto di vista geometrico.
Se, come hai scritto, non hai difficoltà a risolvere il problema dal punto di vista geometrico, tutto quello che ti serve sono dei vettori che contengano le coordinate dei punti che hai calcolato e la funzione plot per plottare la curva come serie di segmenti.
Per impostare in MatLab i calcoli che hai fatto "su carta" ti dovrebbero bastare i semplici operatori aritmetici e, a seconda della complessità della soluzione "geometrica" le funzioni "sin", "cos", "tan".
Se il problema è nell'uso degli operatori di base e le semplici funzioni trigonometriche, forse è il caso che tu dia un'occhiata ai fondamenti del linguaggio (
https://www.mathworks.com/help/pdf_doc/matlab/getstart.pdf)
L'implementazione della soluzione "semplice" potrebbe essere:
r=3;
c=[0 0]
dist_p=2*r;
p1=[c(1)-dist_p*r 0];
p2=[c(1)+dist_p*r 0];
t=0:.01:2*pi;
x=c(1)+r*cos(t);
y=c(2)+r*sin(t);
plot(p1(1),p1(2),'d',p2(1),p2(2),'d',x,y,'k')
daspect([1 1 1])
grid minor
hold on
int_1=[p1(1)+((c(1)-r)-p1(1))/2 c(2)+r*2];
int_2=[p2(1)+((c(1)-r)-p2(1))/2 c(2)+r*2];
plot(int_1(1),int_1(2),'d',int_2(1),int_2(2),'d')
xc=[p1(1) int_1(1) int_2(1) p2(1)];
yc=[p1(2) int_1(2) int_2(2) p2(2)];
plot(xc,yc,'r')
xcyc=p1(1):p2(1)
yy=spline(xc,yc,xcyc);
plot(xcyc,yy,'b')
Allegati:
16082_5863f7386e091461d7c85423813499c2.jpg