Equazioni differenziali a coefficienti non costanti

di
1keenan
il
473 risposte

473 Risposte - Pagina 23

  • G
    giug
    Molto attivo
    Iscritto da
    nov, 2011
    Messaggi:
    641

    Re: Equazioni differenziali a coefficienti non costanti

    Intanto digli di disegnarti i puntini, altrimenti lui li collega con le linee, almeno si capisce come sono messi i punti (non che venga fuori qualcosa di più confortante...)
    plot3(THETA,PHI,R,'.')
    Poi, il codice lo puoi scrivere così, senza il ciclo for (non so se c'è anche un minimo di differenza anche dal punto di vista della "casualità" della funzione rand, nel caso è comunque meglio scriverla così):
    A_ang=-0.08; B_ang=0.08;
teta = A_ang + (B_ang-A_ang) * rand(1000,1); %random number in [A,B]
fi = A_ang + (B_ang-A_ang) * rand(1000,1);
    Insomma, hai due distribuzioni random uniformi comprese tra due valori... a che serve la sfera, cosa vorresti sapere? Essendo distribuzioni uniformi, perché dovrebbero "accumularsi"?
  • 1
    1keenan
    Utente Attivo
    Iscritto da
    gen, 2012
    Messaggi:
    315

    Re: Equazioni differenziali a coefficienti non costanti

    giug ha scritto:


    Insomma, hai due distribuzioni random uniformi comprese tra due valori... a che serve la sfera, cosa vorresti sapere? Essendo distribuzioni uniformi, perché dovrebbero "accumularsi"?

    Scrivo come ha detto tu: 
    
A_ang=-0.08; B_ang=0.08;
teta = A_ang + (B_ang-A_ang) * rand(1000,1); %random number in [A,B]
fi = A_ang + (B_ang-A_ang) * rand(1000,1);
 r=[0:0.001:(1-1.000e-3)]';
 [T,F,R]=cart2sph(teta, fi, r);
plot3(T,F,R,'.')
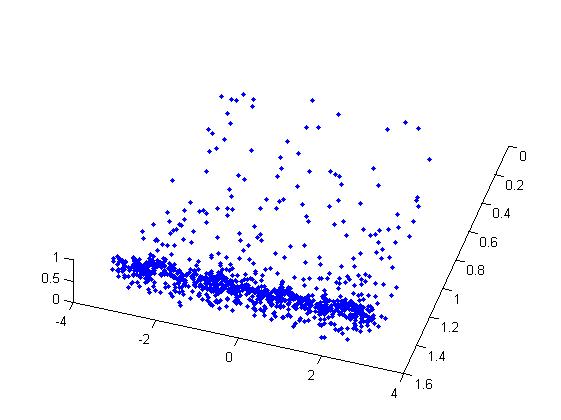
    e dal plot allegato si vede che c'è una zona dove i punti sono meno densi.

    I discorso dovrebbe essere che se io gli faccio estrarre un angolo tra 0 e 360 e l'altro tra -90 e 90 e li plotto sulla sfera di raggio 1, i punti saranno uniformemente distribuiti sui "meridiani" della sfera, ma siccome i meridiani sono più piccoli ai poli qui ci sarà un accumulo di puntini.
    era quello che volevo vedere, ma non lo so fare. se dico: 
    
>> A_ang=0; B_ang=360;
>> teta = A_ang + (B_ang-A_ang) * rand(1000,1); 
>> A_ang=-90;B_ang=90;
>> fi = A_ang + (B_ang-A_ang) * rand(1000,1);
>> r=[0:0.001:(1-1.000e-3)]';
>> [T,F,R]=cart2sph(teta, fi, r);
>> plot3(T,F,R,'.')
    fa una porcheria invece di una nuvoletta sferica...
    Allegati:
    9724_f20937255a6259ada2881c3d62fd2c15.jpg
    9724_f20937255a6259ada2881c3d62fd2c15.jpg
  • G
    giug
    Molto attivo
    Iscritto da
    nov, 2011
    Messaggi:
    641

    Re: Equazioni differenziali a coefficienti non costanti

    Prova a guardare questo: 
    phi = (rand(1000,1)*180-90);
theta = rand(1000,1)*360;
r = 1;
color = rand(1000,1);
[Az El] = meshgrid(0:360,-90:90);
C = griddata(theta,phi,color,Az,El);
[x y z] = sph2cart(Az*pi/180,El*pi/180,r);
surf(x,y,z,C)
axis equal off vis3d
  • G
    giug
    Molto attivo
    Iscritto da
    nov, 2011
    Messaggi:
    641

    Re: Equazioni differenziali a coefficienti non costanti

    Ecco, forse dovrebbe andare bene così...
    phi = (rand(1000,1)*180-90);
theta = rand(1000,1)*360;
r = 1;
[x y z] = sph2cart(phi,theta,r);
plot3(x,y,z,'.');
  • 1
    1keenan
    Utente Attivo
    Iscritto da
    gen, 2012
    Messaggi:
    315

    Re: Equazioni differenziali a coefficienti non costanti

    giug ha scritto:

    Ecco, forse dovrebbe andare bene così...
    phi = (rand(1000,1)*180-90);
theta = rand(1000,1)*360;
r = 1;
[x y z] = sph2cart(phi,theta,r);
plot3(x,y,z,'.');

    se gli dici 10000 anzicchè 1000 si vede quello che ti dicevo prima... pare che la cosa migliore sia fargli fare una nuvoletta quadrata di raggio 1 e levare quei punti per cui non è soddisfatta la condizione x^2+y^2+z^2<=1, che è la sfera di raggio uno.

    la cosa che hai fatto prima è uno spettacolo, poi la guardo bene... ora stiamo sparando per vedere le parabole dal vivo
  • G
    giug
    Molto attivo
    Iscritto da
    nov, 2011
    Messaggi:
    641

    Re: Equazioni differenziali a coefficienti non costanti

    Non l'ho fatta io... non sapevo neanche da dove cominciare... è solo uno dei primi risultati su google se cerchi "plot angle sphere matlab".
    Non riesco ad immaginarmi una nuvola quadrata con un raggio... ma ho capito l'idea. Fai un if, se soddisfa la condizione sei all'interno della sfera.
  • 1
    1keenan
    Utente Attivo
    Iscritto da
    gen, 2012
    Messaggi:
    315

    Re: Equazioni differenziali a coefficienti non costanti

    giug ha scritto:

    Non riesco ad immaginarmi una nuvola quadrata con un raggio... ma ho capito l'idea. Fai un if, se soddisfa la condizione sei all'interno della sfera.
    Non te la immagini perchè la nuvoletta quadrata ha lato 1, io faccio altro e scrivo cacchiate...
    Devo dirgli qualcosa del tipo:
    x=[-0.5:0.00001:0.5];
    y=z=pure;
    if prendi solo i puntini dentro la sfera...

    la distribuzione dovrebbe essere uniforme.
  • G
    giug
    Molto attivo
    Iscritto da
    nov, 2011
    Messaggi:
    641

    Re: Equazioni differenziali a coefficienti non costanti

    Quindi è un cubo? o una sfera?
    comunque, concentrati a fare parabole, questo dovrebbe essere abbastanza semplice.
  • 1
    1keenan
    Utente Attivo
    Iscritto da
    gen, 2012
    Messaggi:
    315

    Re: Equazioni differenziali a coefficienti non costanti

    giug ha scritto:

    quindi è un cubo? o una sfera?
    comunque, concentrati a fare parabole, questo dovrebbe essere abbastanza semplice.

    sì è un cubo e con l'if gli levo gli spigoli e la faccio diventare un cubo.

    Qua abbiamo tre telecamere... tutte e tre scassate... è da stamattina che cerchiamo di acquisire qualcosa ma non acquisiamo nulla...
  • G
    giug
    Molto attivo
    Iscritto da
    nov, 2011
    Messaggi:
    641

    Re: Equazioni differenziali a coefficienti non costanti

    Dormiteci sopra... domani funzionerà tutto...
  • 1
    1keenan
    Utente Attivo
    Iscritto da
    gen, 2012
    Messaggi:
    315

    Re: Equazioni differenziali a coefficienti non costanti

    giug ha scritto:

    Dormiteci sopra... domani funzionerà tutto...
    non penso proprio....
  • 1
    1keenan
    Utente Attivo
    Iscritto da
    gen, 2012
    Messaggi:
    315

    Re: Equazioni differenziali a coefficienti non costanti

    1keenan ha scritto:

    giug ha scritto:

    quindi è un cubo? o una sfera?
    comunque, concentrati a fare parabole, questo dovrebbe essere abbastanza semplice.

    sì è un cubo e con l'if gli levo gli spigoli e la faccio diventare un cubo.
    volevo dire:"sì è un cubo e con l'if gli levo gli spigoli e la faccio diventare una sfera."
  • G
    giug
    Molto attivo
    Iscritto da
    nov, 2011
    Messaggi:
    641

    Re: Equazioni differenziali a coefficienti non costanti

    Sì sì, avevo capito, non volevo mettere il dito nella piaga...
  • 1
    1keenan
    Utente Attivo
    Iscritto da
    gen, 2012
    Messaggi:
    315

    Re: Equazioni differenziali a coefficienti non costanti

    giug ha scritto:

    sì sì, avevo capito, non volevo mettere il dito nella piaga...
    grazie per la comprensione.

    Domani provo sta cosa del cubo, solo che se gli dico:
    x=[-1:0.00001:1];
    y=z=pure;
    if prendi solo i puntini dentro la sfera.

    lui la sfera la fa piena, non fa solo la superfice... quindi la condizione non può essere x^2+y^2+z^2<=1, deve essere ==1...bho, domani si pensa.
  • G
    giug
    Molto attivo
    Iscritto da
    nov, 2011
    Messaggi:
    641

    Re: Equazioni differenziali a coefficienti non costanti

    Ti serve solo la superficie? In quel caso devi stabilire una specie di fascia di tolleranza attorno alla superficie della sfera.
    Prima stavo anche dando un'occhiata alla funzione sphere, che costruisce una superficie sferica. Non so se però può tornare utile in questo caso, se può essere usata per definire l'appartenenza di alcuni punti alla superficie stessa.
Devi accedere o registrarti per scrivere nel forum
473 risposte