giug ha scritto:
una splendida rappresentazione della non-correlazione...
Buon giorno.
Sono stato in eremitaggio sul pizzo della montagna ed ho riflettuto:
intanto la condizione di selezione delle particelle è sbagliata perchè noi abbiamo messo:
if (abs(ys(end,1)) <=r_pin1 || abs(ys(end,2))<=r_pin1)
....
mentre in realtà dovrebbe essere &&, giusto? (volendo selezionare le particelle che passano dal diaframma devo prendere quelle le cui coordinare ys(end,1) e ys(end,2) sono entrambe minori del raggio del buco, non basta che solo una sia minore... quindi serve and invece di or)
Poi se gli angoli li prendo uguali il fascio, visto di fronte (come se mettessi l'occhio sul diaframma) è una retta. questo non va bene perchè gli angoli effettivamente devono essere indimendento, quindi gli dico:
angolo1 = A_ang + (B_ang-A_ang) * rand(1); %random number in [A,B]
angolo2 = A_ang + (B_ang-A_ang) * rand(1);
teta=angolo1; %angolo nel piano zy
fi=angolo2; %angolo con l'asse x
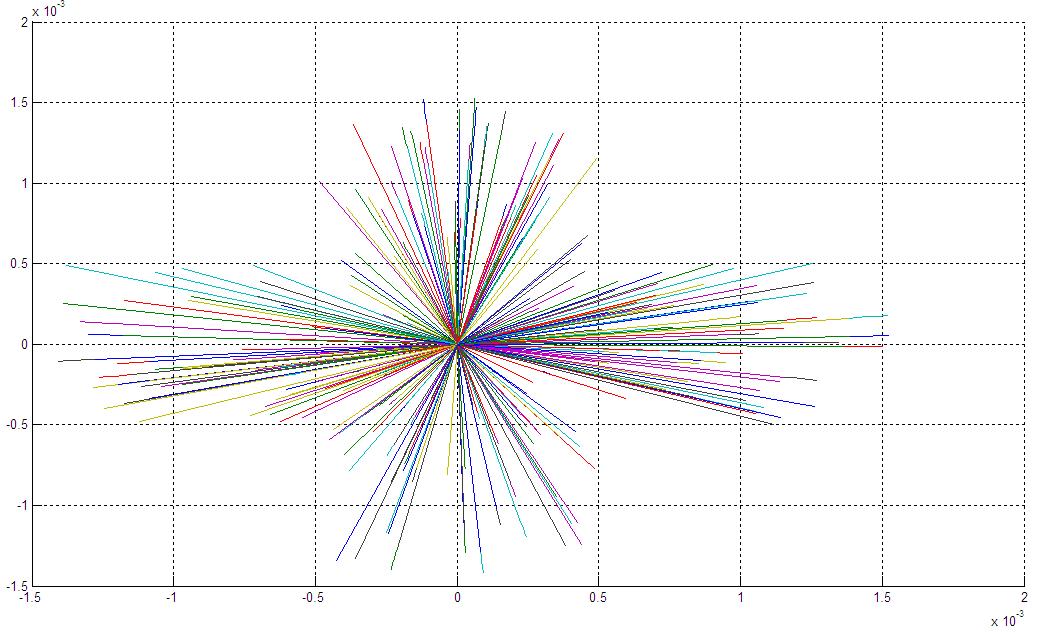
da un lato la cosa migliora, ma dall'altro fa una cosa strana che mi fa pensare che questa estrazione angolare non è fatta bene.
La sezione del fascio sembra il simbolo "fiori" delle carte francesi con un pò di fantasia, mentre io me la aspetto tonda, ti allego l'immagine.
Volevo provare a plottare sti angoli su una superfice sferica perchè secondo me si addensano da qualche parte in questo modo o comunque su una sfera non sono uniformi...
Allegati:
9724_9a1850b17a8ed5043876575a9d7f7ec7.jpg