Allora, ho fatto la prova così (scusa, non ho resistito, ero curiosa...)
Ho lanciato il vecchio codice. Poi ho assegnato la struttura ad un altra per non sovrascriverla
Particella1=Particella;
Poi ho cancellato le variabili che sarebbero cambiate con le modifiche, quindi:
clear Particella v_x v_y v_z v_ion y_sorgente.
Poi con un ciclo come questo ho confrontato tutti i campi della struttura:
for i = 1:300
x(i)=isequal(Particella(i).velocita,Particella1(i).velocita);
end
find(x==0)
x è uguale a 1 se i due campi sono diversi.
Le traiettorie hanno qualche campo che risulta diverso ma sembrano problemi di arrotondamento (in un caso mette 1, nell'altro 1.0000)
Le velocità invece vengono tutte diverse. Ma vengono diverse anche se lanci lo stesso codice 2 volte. Quindi
Particella2=Particella;
e ho rilanciato lo stesso codice (quello modificato) e ho fatto la stessa verifica.
Quindi Particella1 è dal codice vecchio, Particella2 e Particella è dal codice nuovo.
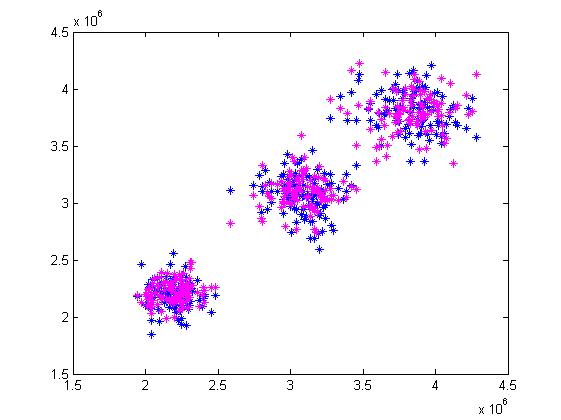
Ora ho fatto dei plot. Ho plottato prima Particella1 con Particella2 (dati dai due codici diversi) e poi Particella e Particella2.
for i = 1:300
plot(Particella2(i).velocita(1,3),Particella(i).velocita(1,3),'*m');hold on;
end
Più o meno mi aspetto che il grafico sia intorno alla bisettrice del quadrante il che vorrebbe dire che sono uguali i numeri confrontati.
Nell'allegato c'è il risultato.
Allegati:
9528_862bfa3b6112f173328cd8ae25786485.jpg