giug ha scritto:
Bella domanda...
ce ne sono? j arriva a 3?
s = 3, ma lui non ne fa passare prima, quando fa la storia della collimazione... bho?
però questo dopo, adesso c'è la legenda che rompe.
Se io scrivo:
figure()
%%%%voglio fare un plot tenendo fisse le dimensioni delle icone nella legenda
cmap = hsv(stati); %# Creates a j-by-3 set of colors from the HSV colormap
legendtext ='';
ion_sym = input ('Simbolo ione da simulare: ', 's');
for j=1:s
for i=1:p
if (Part_trasp(i).ionizzazione == j)
B_defl(i) = Part_trasp(i).traiettoria(end,2);
E_defl(i) = Part_trasp(i).traiettoria(end,1);
hplot(j) = plot(B_defl(:,j), E_defl(:,j),'*','Color',cmap(j,:),'Markersize', 10);
%'Color',cmap(j,:) %# Plot each column with a different color
hold on
end
end
legendtext = [legendtext; ion_sym, '^{', num2str(j),'+}'];
%hold on
end
hold on
plot(Ymcporigine,Xmcporigine,'k-','MarkerEdgeColor','k','MarkerSize',1); %Plot contorno MCP
%Label assi principali - It is necessary to give the label instructions after plot in order to avoid overlap
xlabel(gca, 'Deflessione magnetica [m]'); % label lower x axis
ylabel(gca,'Deflessione elettrica [m]'); %label left y axis
%particles outside MCP radius won't appear in figure
xlim([0, Rmcp])
ylim([0, Rmcp])
% %%%% legenda assi principali
l=legend(legendtext, 'Location', 'BestOutside');
a=get(l, 'children');
set(a(1:3:end),'MarkerSize', 10);
% %
% %%%% doppi Assi
%set secondary x limit as the momentum of a H+ at distance equal to the MCP radius
% Secondo Harres y=(q*B*LB*L)/sqrt(2mEkin) ==> mv=q*B*LB*L/y
%L=Deriva2;
L=0.46;
CB=0.006;
mv_max = (q*CB*LB*L)/Rmcp;
%mv_max = 1;
%set secondary y limit as the energy of a H+ at distance equal to the MCP radius
% Secondo Harres x=(q*E*Le*L)/(2Ekin) ==> Ekin=q*E*Le*L/2x
Le = 0.07; %Estensione del C.E. : 70 mm
CE = 100000; %campo TP.m
Ekin_max = ((q*CE*Le*L)/(2*Rmcp))/eV;
%mv_max = 1;
%Layout instruction
set(gca,'Box','off'); % Turn off the box surrounding the whole axes
axesUnits=get(gca,'Units');
axesPosition = get(gca,'Position'); %# Get the current axes position
hNewAxes = axes('Position', axesPosition,... %# Place a new axes on top...
'Units', 'normalized',...
'ActivePositionProperty', 'Position',... %prova anche OuterPosition
'Color','none',... %# ... with no background color
'YAxisLocation', 'right',...
'XAxisLocation','top',... %# ... located on the top
'Ylim', [0, Ekin_max],...
'Xlim', [0, mv_max],... %# ... should define x axis scale (need to set xmax = mv_max)
'Box','off'); %# ... and no surrounding box
xlabel(hNewAxes,'Momentum (H^+)'); %# Add a label to the top axis
ylabel(hNewAxes,'Energy (H^+)'); %# Add a label to the right axis
set(gca, 'XTickLabel', num2str(get(gca,'XTick')','%g'))
set(gca, 'YTickLabel', num2str(get(gca,'YTick')','%g'))
lui mi fa i marker della legenda tutti dello stesso colore, almeno credo...(allegato screenshot)
Se la metto prima lui mi fa una legenda dove compaiono tutte le particelle, una striscia lunghissima....
BASTAAAA!!
Allegati:
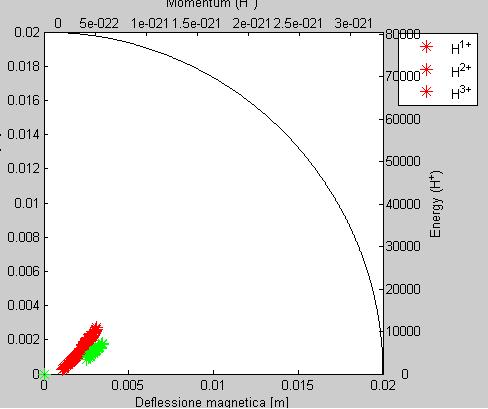9724_6e47f9408d2f0752007c85803557b47b.jpg