Per quanto riguarda il primo problema (NaN et -Inf) servirebbero i dati di input per fare qualche prova.
Potresti pubblicare un esempio significativo dei dati di input o condividerli in un repository (es. dropbox, ...)?
Per quanto riguarda le funzioni:
"polyfit" ritorna i coefficienti di un polinomio di grado "n" (specificato come terzoparametro nella chiamata alla funzione) nel tuo caso:
logp1 = polyfit(x,log10(y),1)
genera i coefficienti di un poolinomio di primo grado, di conseguenza, la funzione non è
y = -0.9056+e^(0.0037 * x)
ma,
y = logp1(1)*x+logp1(2)
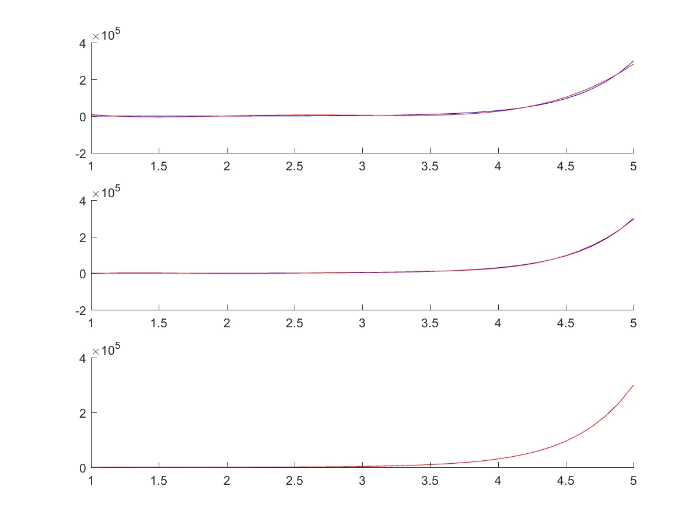
Non avendo (al momento) a disposizione i dati di input, un esempio potrebbe essere:
% Generazione dati di input
x=1:.1:5
y=3*10.^x
% Interpolazione con polinomio 4° grado
subplot(3,1,1)
c=polyfit(x,y,4)
k=polyval(c,x)
hold on
plot(x,y,'b',x,k,'r')
% Interpolazione con polinomio 5° grado
subplot(3,1,2)
c=polyfit(x,y,5)
k=polyval(c,x)
hold on
plot(x,y,'b',x,k,'r')
% Interpolazione con polinomio 7° grado
subplot(3,1,3)
c=polyfit(x,y,7)
k=polyval(c,x)
hold on
plot(x,y,'b',x,k,'r')
Allegati:
 16082_7e3402939bb0766111bde148c5f77cdc.jpg
16082_7e3402939bb0766111bde148c5f77cdc.jpg