Nell’articolo precedente abbiamo visto che cosa sono la regressione lineare e la regressione polinomiale, da un punto di vista più teorico-matematico.
Vediamo ora un esempio pratico di tracciamento di un grafico in grado di rappresentare una relazione lineare tra diverse coppie di valori, poi vedremo un esempio simile con una regressione polinomiale.
Regressione lineare
Supponiamo di voler prevedere il prezzo di vendita di una casa in base alla sua superficie, basandoci sui dati seguenti:
Superficie (m²) | Prezzo (EUR) |
50 | 180,000 |
60 | 210,000 |
70 | 240,000 |
80 | 270,000 |
90 | 300,000 |
Utilizzando la regressione lineare, possiamo determinare la relazione tra la superficie e il prezzo.
Supponiamo che l'equazione trovata sia:
Prezzo = 30000 + 3000 × Superficie
Proviamo a utilizzare il codice C# per visualizzare il grafico di questa relazione.
Per semplicità creeremo una applicazione di tipo Windows Forms, per cui potete creare voi stessi una nuova applicazione con questo modello. Una volta pronta, sostituite tutto il codice contenuto nel file Program.cs con quello seguente:
// Regressione lineare in C#
using System;
using System.Collections.Generic;
using OxyPlot;
using OxyPlot.Series;
class Program
{
static void Main(string[] args)
{
// Dati
List<double> superficie = new List<double> { 50, 60, 70, 80, 90 };
List<double> prezzo = new List<double> { 180000, 210000, 240000, 270000, 300000 };
// Coefficienti della retta di regressione
double beta_0 = 30000;
double beta_1 = 3000;
// Calcolo della retta di regressione
List<double> retta_regressione = new List<double>();
foreach (double x in superficie)
{
retta_regressione.Add(beta_0 + beta_1 * x);
}
// Creazione del grafico utilizzando OxyPlot
var plotModel = new PlotModel { Title = "Regressione Lineare: Superficie vs Prezzo" };
var scatterSeries = new ScatterSeries { MarkerType = MarkerType.Circle, MarkerFill = OxyColors.Blue };
for (int i = 0; i < superficie.Count; i++)
{
scatterSeries.Points.Add(new ScatterPoint(superficie[i], prezzo[i]));
}
var lineSeries = new LineSeries { Color = OxyColors.Red };
for (int i = 0; i < superficie.Count; i++)
{
lineSeries.Points.Add(new DataPoint(superficie[i], retta_regressione[i]));
}
plotModel.Series.Add(scatterSeries);
plotModel.Series.Add(lineSeries);
// Mostra il grafico (è necessario un visualizzatore per grafici OxyPlot)
var plotView = new OxyPlot.WindowsForms.PlotView
{
Model = plotModel,
Dock = System.Windows.Forms.DockStyle.Fill
};
var form = new System.Windows.Forms.Form { ClientSize = new System.Drawing.Size(800, 600) };
form.Controls.Add(plotView);
System.Windows.Forms.Application.Run(form);
}
}
Noterete sicuramente che in alcune istruzioni vengono identificati degli errori. Il motivo è piuttosto semplice: è necessario aggiungere una libreria di nome Oxyplot. Per svolgere questa operazione potete aprire la voce di menu Strumenti > Gestione pacchetti NuGet > Console di Gestione Pacchetti (o in inglese Tools > NuGet Package Manager > Package Manager Console) e digitare nella console il comando seguente:
Install-Package OxyPlot.WindowsForms
Qualche istante di attesa e tutti gli errori saranno risolti, permettendoci di eseguire il programma e di ottenere il seguente risultato (Fig. 1):
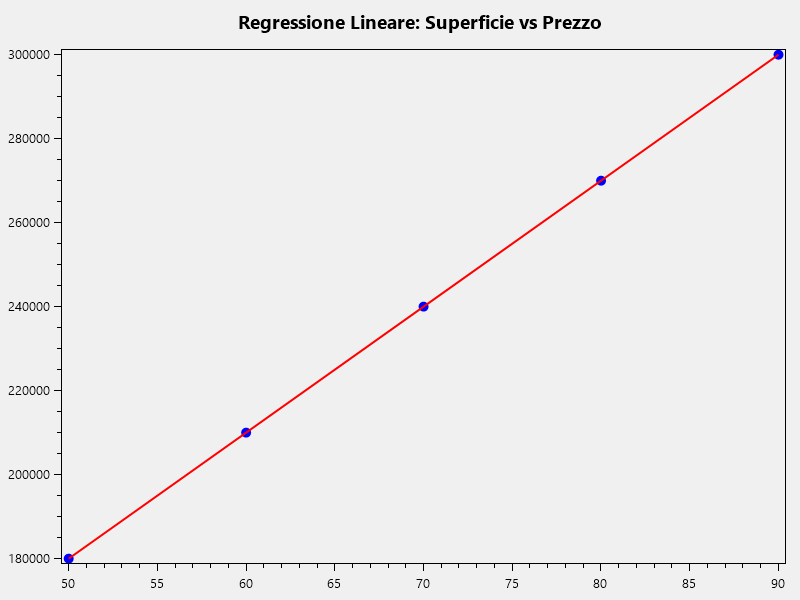
In questo caso possiamo vedere che la retta passa esattamente sui punti, proprio perché esiste una relazione lineare e quindi esiste anche una retta in grado di rappresentare qualsiasi valore secondo l’equazione data.
Regressione polinomiale
Vediamo ora cosa succede con una nuova serie di dati e utilizzando una regressione polinomiale di secondo grado:
Superficie (m²) | Prezzo (EUR) |
50 | 150,000 |
60 | 175,000 |
70 | 200,000 |
80 | 240,000 |
90 | 300,000 |
Noterete sicuramente che alcuni prezzi sono stati modificati: tra poco sarà evidente come questi sono disposti su una curva crescente.
Creiamo una applicazione Windows Forms e sostituiamo il codice di Program.cs con il seguente:
// Regressione polinomiale in C#
using System;
using System.Collections.Generic;
using OxyPlot;
using OxyPlot.Series;
using MathNet.Numerics.LinearRegression;
class Program
{
static void Main(string[] args)
{
// Dati
double[] superficie = { 50, 60, 70, 80, 90 };
double[] prezzo = { 150000, 175000, 200000, 240000, 300000 };
// Trasformazione polinomiale di grado 2
double[][] superficie_poly = new double[superficie.Length][];
for (int i = 0; i < superficie.Length; i++)
{
superficie_poly[i] = new double[] { 1, superficie[i], superficie[i] * superficie[i] };
}
// Modello di regressione polinomiale
var result = MultipleRegression.QR(superficie_poly, prezzo);
// Predizioni
double[] prezzo_predetto = new double[superficie.Length];
for (int i = 0; i < superficie.Length; i++)
{
prezzo_predetto[i] = result[0] + result[1] * superficie[i] + result[2] * superficie[i] * superficie[i];
}
// Creazione del grafico utilizzando OxyPlot
var plotModel = new PlotModel { Title = "Regressione Polinomiale: Superficie vs Prezzo" };
var scatterSeries = new ScatterSeries { MarkerType = MarkerType.Circle, MarkerFill = OxyColors.Blue };
for (int i = 0; i < superficie.Length; i++)
{
scatterSeries.Points.Add(new ScatterPoint(superficie[i], prezzo[i]));
}
var lineSeries = new LineSeries { Color = OxyColors.Red };
for (int i = 0; i < superficie.Length; i++)
{
lineSeries.Points.Add(new DataPoint(superficie[i], prezzo_predetto[i]));
}
plotModel.Series.Add(scatterSeries);
plotModel.Series.Add(lineSeries);
// Mostra il grafico (è necessario un visualizzatore per grafici OxyPlot)
var plotView = new OxyPlot.WindowsForms.PlotView
{
Model = plotModel,
Dock = System.Windows.Forms.DockStyle.Fill
};
var form = new System.Windows.Forms.Form { ClientSize = new System.Drawing.Size(800, 600) };
form.Controls.Add(plotView);
System.Windows.Forms.Application.Run(form);
}
}
In questo caso dovete aggiungere la libreria Oxyplot, ma anche una libreria che si chiama MathNet.Numerics che ci servirà per utilizzare la sua classe MultipleRegression.
Install-Package MathNet.Numerics
Ecco, quindi, cosa otteniamo dai dati utilizzati:
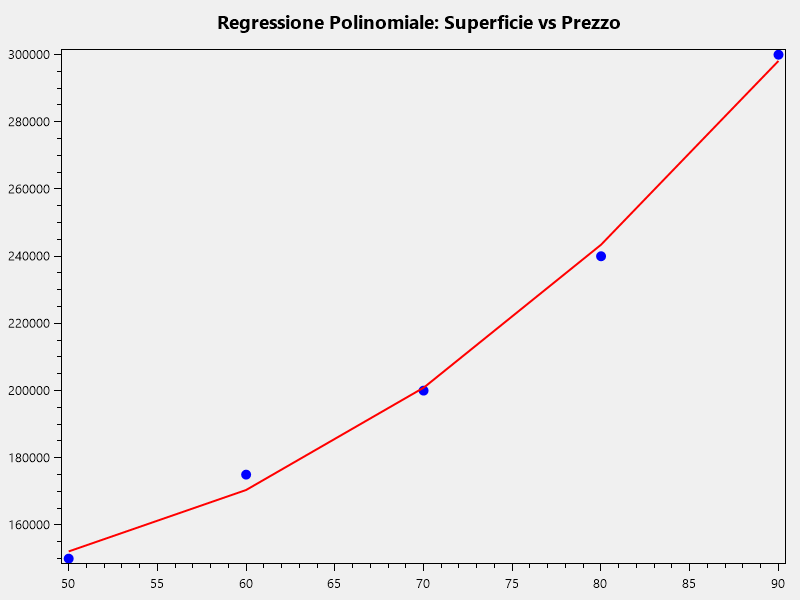
Come potete notare, la curva (per semplicità rappresentata da segmenti) non passa esattamente sui punti: infatti l’obiettivo non è quello di trovare esattamente la curva su cui passano tutti i punti (anche perché molto probabilmente non esiste una curva esatta), bensì di trovare la curva che è in grado di approssimare il più possibile l’andamento dei dati, per poter stimare dei valori non presenti nella tabella.
Conclusione
Ovviamente questo è solo un piccolo esempio, per poter comprendere come si possono ottenere informazioni utili dai dati ed essere in grado di formulare delle previsioni, seppure accettando un piccolo grado di errore (come spesso avviene in molti ambiti di lavoro).
Una intelligenza artificiale è in grado di determinare la curva più appropriata, utilizzando una delle tecniche di regressione, e quindi di fare una previsione basata su un valore fornito dall’utente, anche se nei dati forniti nella fase di training quel valore non c’è.