Overfitting e underfitting

In machine learning, uno degli obiettivi principali è creare modelli che possano generalizzare bene sui dati che il sistema non conosce, cioè dati che non sono stati utilizzati durante l'addestramento del modello. Due problemi comuni che ostacolano questo obiettivo sono l'overfitting e l'underfitting. Vediamo di cosa si tratta.

Overfitting

In fase di training può capitare che il modello sia troppo complesso e che si adatti troppo bene ai dati utilizzati, catturando non solo gli schemi generali ma anche il “rumore” e le caratteristiche specifiche dei dati. Di conseguenza, il modello ha delle prestazioni eccellenti sui dati di training, ma prestazioni scarse sui dati di test o sui nuovi dati.

Sintetizzando, in questo caso abbiamo:

• un errore di addestramento molto basso ed un errore di test alto;
• un modello con troppi parametri rispetto alla quantità di dati disponibili;
• oscillazioni significative nei parametri del modello.

Per risolvere questo problema si può:

• ridurre la complessità del modello: utilizzare modelli con meno parametri;
• aumentare la quantità di dati: più dati possono aiutare a stabilizzare i parametri del modello e a rendere il modello meno incline a catturare il “rumore”;
• cross-validation: utilizzare tecniche di validazione incrociata per verificare le prestazioni del modello su più suddivisioni del dataset;
• regolarizzazione: tecniche come L1, L2 e dropout (per le reti neurali) aiutano a penalizzare la complessità del modello.

Underfitting

Questo problema è sostanzialmente l’opposto di quello che abbiamo visto precedentemente.

Si verifica quando un modello è troppo semplice per catturare gli schemi presenti nei dati. Il modello ha prestazioni scarse sia sui dati di addestramento che sui dati di test, indicando che non ha imparato abbastanza dai dati disponibili.

In questo caso abbiamo:

• sia un errore di addestramento, sia un errore di test alti;
• il modello non è in grado di catturare le tendenze generali dei dati;
• prestazioni scarse anche sui dati di addestramento.

Per risolvere un problema di underfitting si può:

• aumentare la complessità del modello: utilizzare modelli più complessi o aggiungere più parametri;
• ridurre il bias: utilizzare algoritmi con un bias inferiore, in grado di adattarsi meglio ai dati;
• feature engineering: aggiungere nuove variabili che possano aiutare il modello a catturare meglio gli schemi nei dati.

Esempio di overfitting e di underfitting

Riprendiamo gli esempi di codice dei precedenti articoli (ved. Regressione lineare e polinomiale) per capire cosa succede quando utilizziamo gli stessi dati per addestrare un modello in una condizione di overfitting, in un caso appropriato e in un caso di underfitting:

“Consideriamo un semplice esempio di previsione del prezzo delle case in base alla loro superficie. Utilizzeremo un set di dati con poche osservazioni per dimostrare sia l'overfitting che l'underfitting.”

Nel linguaggio C# potremmo avere un codice come il seguente:

using System;
using System.Collections.Generic;
using OxyPlot;
using OxyPlot.Series;
using MathNet.Numerics.LinearRegression;
using MathNet.Numerics;

class Program
{
    static void Main(string[] args)
    {
        // Dati
        double[] superficie = { 50, 60, 70, 80, 90 };
        double[] prezzo = { 150000, 175000, 200000, 240000, 300000 };

        // Modello Lineare (Underfitting)
        var linearModel = Fit.Line(superficie, prezzo);

        // Modello Polinomiale di grado 2 (Appropriato)
        var polyModel2 = Fit.Polynomial(superficie, prezzo, 2);

        // Modello Polinomiale di grado 10 (Overfitting)
        var polyModel10 = Fit.Polynomial(superficie, prezzo, 10);

        // Predizioni
        double[] y_pred_linear = new double[superficie.Length];
        double[] y_pred_poly_2 = new double[superficie.Length];
        double[] y_pred_poly_10 = new double[superficie.Length];

        for (int i = 0; i < superficie.Length; i++)
        {
            y_pred_linear[i] = linearModel.Item1 + linearModel.Item2 * superficie[i];
            y_pred_poly_2[i] = polyModel2[0] + polyModel2[1] * superficie[i] + polyModel2[2] * superficie[i] * superficie[i];
            y_pred_poly_10[i] = 0;
            for (int j = 0; j <= 10; j++)
            {
                y_pred_poly_10[i] += polyModel10[j] * Math.Pow(superficie[i], j);
            }
        }

        // Creazione del grafico utilizzando OxyPlot
        var plotModel = new PlotModel { Title = "Esempio di Overfitting e Underfitting" };

        var scatterSeries = new ScatterSeries { MarkerType = MarkerType.Circle, MarkerFill = OxyColors.Blue };
        for (int i = 0; i < superficie.Length; i++)
        {
            scatterSeries.Points.Add(new ScatterPoint(superficie[i], prezzo[i]));
        }

        var lineSeriesLinear = new LineSeries { Color = OxyColors.Green, Title = "Lineare (Underfitting)" };
        for (int i = 0; i < superficie.Length; i++)
        {
            lineSeriesLinear.Points.Add(new DataPoint(superficie[i], y_pred_linear[i]));
        }

        var lineSeriesPoly2 = new LineSeries { Color = OxyColors.Red, Title = "Polinomiale Grado 2" };
        for (int i = 0; i < superficie.Length; i++)
        {
            lineSeriesPoly2.Points.Add(new DataPoint(superficie[i], y_pred_poly_2[i]));
        }

        var lineSeriesPoly10 = new LineSeries { Color = OxyColors.Purple, Title = "Polinomiale Grado 10 (Overfitting)" };
        for (int i = 0; i < superficie.Length; i++)
        {
            lineSeriesPoly10.Points.Add(new DataPoint(superficie[i], y_pred_poly_10[i]));
        }

        plotModel.Series.Add(scatterSeries);
        plotModel.Series.Add(lineSeriesLinear);
        plotModel.Series.Add(lineSeriesPoly2);
        plotModel.Series.Add(lineSeriesPoly10);

        // Mostra il grafico (è necessario un visualizzatore per grafici OxyPlot)
        var plotView = new OxyPlot.WindowsForms.PlotView
        {
            Model = plotModel,
            Dock = System.Windows.Forms.DockStyle.Fill
        };

        var form = new System.Windows.Forms.Form { ClientSize = new System.Drawing.Size(800, 600) };
        form.Controls.Add(plotView);
       System.Windows.Forms.Application.Run(form);
    }
}

Nel linguaggio Python avremmo questo codice:

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
from sklearn.metrics import mean_squared_error

# Dati
X = np.array([50, 60, 70, 80, 90]).reshape(-1, 1)
y = np.array([150000, 175000, 200000, 240000, 300000])

# Regressione Lineare (Underfitting)
linear_model = LinearRegression()
linear_model.fit(X, y)
y_pred_linear = linear_model.predict(X)

# Regressione Polinomiale di grado 2 (Appropriata)
poly_features_2 = PolynomialFeatures(degree=2)
X_poly_2 = poly_features_2.fit_transform(X)
poly_model_2 = LinearRegression()
poly_model_2.fit(X_poly_2, y)
y_pred_poly_2 = poly_model_2.predict(X_poly_2)

# Regressione Polinomiale di grado 10 (Overfitting)
poly_features_10 = PolynomialFeatures(degree=10)
X_poly_10 = poly_features_10.fit_transform(X)
poly_model_10 = LinearRegression()
poly_model_10.fit(X_poly_10, y)
y_pred_poly_10 = poly_model_10.predict(X_poly_10)

# Creazione del grafico
plt.scatter(X, y, color='blue', label='Dati osservati')

plt.plot(X, y_pred_linear, color='green', label='Lineare (Underfitting)')
plt.plot(X, y_pred_poly_2, color='red', label='Polinomiale Grado 2')
plt.plot(X, y_pred_poly_10, color='purple', label='Polinomiale Grado 10 (Overfitting)')

plt.xlabel('Superficie (m²)')
plt.ylabel('Prezzo (EUR)')
plt.title('Esempio di Overfitting e Underfitting')
plt.legend()
plt.grid(True)
plt.show()

# Calcolo dell'errore
print("Errore Lineare:", mean_squared_error(y, y_pred_linear))
print("Errore Polinomiale Grado 2:", mean_squared_error(y, y_pred_poly_2))
print("Errore Polinomiale Grado 10:", mean_squared_error(y, y_pred_poly_10))

Infine, in R avremmo questo codice:

# Dati
superficie <- c(50, 60, 70, 80, 90)
prezzo <- c(150000, 175000, 200000, 240000, 300000)

# Creazione del data frame
dati <- data.frame(superficie, prezzo)

# Modello Lineare (Underfitting)
modello_lineare <- lm(prezzo ~ superficie, data = dati)

# Modello Polinomiale di grado 2 (Appropriato)
modello_poly_2 <- lm(prezzo ~ poly(superficie, 2), data = dati)

# Modello Polinomiale di grado 10 (Overfitting)
modello_poly_10 <- lm(prezzo ~ poly(superficie, 10), data = dati)

# Predizioni
dati$prezzo_pred_lineare <- predict(modello_lineare, newdata = dati)
dati$prezzo_pred_poly_2 <- predict(modello_poly_2, newdata = dati)
dati$prezzo_pred_poly_10 <- predict(modello_poly_10, newdata = dati)

# Creazione del grafico
plot(dati$superficie, dati$prezzo, main="Esempio di Overfitting e Underfitting", 
     xlab="Superficie (m²)", ylab="Prezzo (EUR)", pch=19, col="blue")
lines(dati$superficie, dati$prezzo_pred_lineare, col="green", lwd=2)
lines(dati$superficie, dati$prezzo_pred_poly_2, col="red", lwd=2)
lines(dati$superficie, dati$prezzo_pred_poly_10, col="purple", lwd=2)
legend("topleft", legend=c("Lineare (Underfitting)", "Polinomiale Grado 2", "Polinomiale Grado 10 (Overfitting)"), 
       col=c("green", "red", "purple"), lty=1, cex=0.8)
grid()

Il grafico risultante sarebbe simile alla seguente immagine:

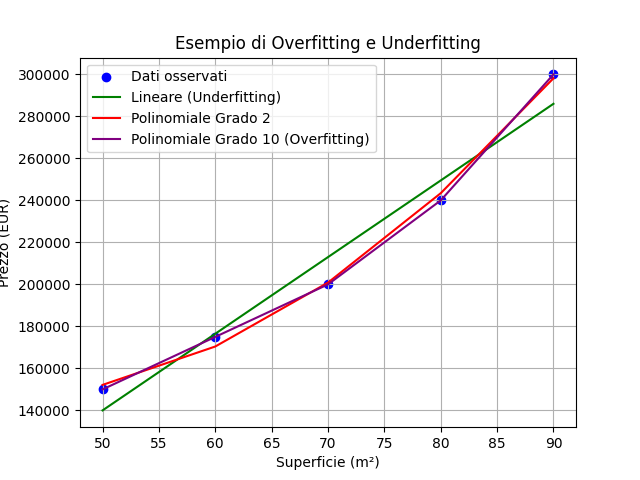
Conclusione

L'underfitting e l'overfitting sono due problemi comuni nella costruzione di modelli di machine learning. È essenziale trovare un equilibrio tra complessità e generalizzazione per creare modelli efficaci e robusti.