Regressione lineare e polinomiale : Introduzione

In questo articolo faremo la conoscenza della regressione lineare e della regressione polinomiale, utilizzate in statistica, in economia, in ingegneria e in molti altri campi applicativi per fare previsioni e comprendere le dinamiche dei dati.

Cercheremo di restare abbastanza “leggeri” senza appesantire eccessivamente con teoremi matematici e senza utilizzare formule eccessivamente complesse, perché l’obiettivo è solo quello di comprendere l’utilità di questi strumenti nel campo dell’intelligenza artificiale.

A margine, dobbiamo osservare che c’è un “contatto” molto forte anche con la Business Intelligence, perché i due mondi si stanno avvicinando molto rapidamente. Infatti, l’intelligenza artificiale può essere utilizzata in modo proficuo per accedere a una grande massa di dati, per analizzarli e ricavare informazioni e correlazioni che per la nostra mente sono difficili da rilevare.

Nel prossimo articolo vi presenteremo degli esempi di codice per poter provare con mano queste importanti tecniche di previsione, ma intanto cerchiamo di capire di cosa stiamo parlando.

Regressione, questa sconosciuta

In realtà non è così sconosciuta, perché chiunque abbia studiato matematica o analisi a un certo livello si è scontrato con la necessità di studiare questa tecnica.

La regressione lineare è una tecnica statistica che viene utilizzata per modellare la relazione tra una variabile dipendente e una o più variabili indipendenti. Sintetizzando, possiamo dire che nella relazione y = f(x), la “x” è la variabile indipendente, mentre la “y” è la variabile dipendente, perché il valore di quest’ultima dipende dal valore della variabile “x” (e ovviamente anche dal tipo di funzione applicata).

La regressione polinomiale è un'estensione della regressione lineare e permette di modellare la relazione tra la variabile dipendente e una o più variabili indipendenti come un polinomio di grado n. Questo metodo è particolarmente utile quando la relazione tra le variabili non è lineare, permettendo di catturare meglio la complessità dei dati.

Nell’ambito dell’intelligenza artificiale le due tipologie di regressione possono essere utilizzate in modo efficace, ma le applicazioni variano a seconda della natura del problema e dei dati.

Regressione Lineare nell'IA

La regressione lineare è spesso utilizzata in IA per i seguenti motivi:

1. semplicità e interpretabilità: la regressione lineare è semplice da implementare e i suoi risultati sono facilmente interpretabili, il che è utile per spiegarne i modelli;
2. modello di riferimento: viene spesso utilizzata come modello basilare per confrontare le prestazioni di modelli più complessi;
3. linearità: è adatta quando si ha una relazione lineare tra la variabile dipendente e le variabili indipendenti;
4. tempo di esecuzione: è economica dal punto di vista computazionale ed è, quindi, adatta per grandi set di dati con molte variabili.

Esempi di utilizzo:

• previsioni di vendite basate su fattori come il prezzo e la pubblicità;
• modelli predittivi semplici in ambito finanziario per prevedere il valore futuro delle azioni;
• analisi di sensibilità per capire l'impatto di diverse variabili indipendenti su una variabile dipendente.

Regressione Polinomiale nell'IA

La regressione polinomiale è utilizzata quando la relazione tra le variabili non è lineare: per esempio nella modellazione di curve e in problemi specifici in cui un polinomio di basso grado (per esempio quadratico) è sufficiente per catturare la complessità dei dati. 

Tuttavia, nella pratica dell'IA, la regressione polinomiale è meno comune rispetto a tecniche più avanzate. I motivi sono abbastanza evidenti:

1. overfitting: aumentando il grado del polinomio, c'è un maggiore rischio di overfitting, cioè il modello si adatta troppo bene ai dati di addestramento ma si generalizza male su nuovi dati;
2. complessità: la complessità dei modelli polinomiali aumenta con il grado del polinomio, rendendo più difficile l'interpretazione e la gestione;
3. alternative: esistono metodi più avanzati e flessibili per modellare relazioni non lineari.

Nell'intelligenza artificiale si preferiscono altre tecniche per modellare relazioni complesse e non lineari:

1. reti neurali: modelli altamente flessibili che possono apprendere relazioni non lineari complesse tra le variabili. Sono alla base di molte applicazioni moderne di intelligenza artificiale, come il riconoscimento delle immagini e il processamento del linguaggio naturale (NLP);
2. alberi decisionali e random forest: sono capaci di gestire relazioni non lineari e interazioni tra variabili in modo intuitivo e visualizzabile;
3. Support Vector Machines (SVM): possono utilizzare kernel non lineari per modellare relazioni complesse;
4. regressione logistica: spesso utilizzata per problemi di classificazione binaria.

L'obiettivo della regressione lineare o polinomiale è trovare i valori di ß₀ e ß₁ (fino a ß_n  nella polinomiale) che minimizzano la somma dei quadrati degli errori (epsilon). Questo è noto come metodo dei minimi quadrati.

Regressione lineare semplice e multipla

La regressione lineare semplice considera una sola variabile indipendente. L'equazione della regressione lineare semplice è:

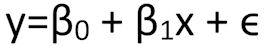
dove:

• y è la variabile dipendente.
• x è la variabile indipendente.
• ß₀ è l'intercetta dell'equazione, cioè il valore di y quando x è zero.
• ß₁ è il coefficiente di regressione, che rappresenta il cambiamento medio di y per un'unità di cambiamento in x.
• epsilon è l'errore o la distorsione, cioè la differenza tra i valori osservati e quelli previsti dal modello.

La regressione lineare multipla estende il concetto di regressione lineare semplice a più variabili indipendenti. L'equazione della regressione lineare multipla è:

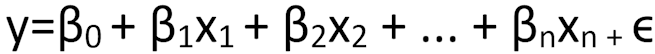
dove abbiamo più coefficienti moltiplicatori delle “n” variabili indipendenti.

In entrambi i modelli, i coefficienti di regressione (ß) rappresentano l'effetto stimato di ogni variabile indipendente sulla variabile dipendente, assumendo che tutte le altre variabili rimangano costanti.

Conclusione

Sia la regressione lineare che quella polinomiale hanno il loro posto nell'arsenale delle tecniche di intelligenza artificiale, ma il loro utilizzo dipende fortemente dalla natura dei dati e dal problema specifico. Mentre la regressione lineare rimane un metodo di base per problemi semplici e lineari, la regressione polinomiale è più limitata e spesso sostituita da tecniche più avanzate per problemi complessi e non lineari.